Hey everyone! I’ve quickly researched using random numbers from within a smart contract for an app I’m developing. I’m sharing it here for two reasons:
- I’d appreciate it if someone with more expertise could review the steps and methods and let me know if anything could have affected the results and how to improve it.
- It could benefit other projects using a similar approach.
I’m building an app on Stacks that uses the VRF seed for an on-chain drawing mechanism. The smart contract responsible for the drawing has a feature that lets it determine the “difficulty” of its drawing. It will accept a difficulty setting from 1 to 10, which will correlate to the chances someone will have of guessing the number the drawing mechanism selected. For a given difficulty d, the chances should be 1/10^d.
It works in two steps:
- Grab the VRF seed for a given block height (tenure height post-Nakamoto) where you want the drawing to happen, and apply the necessary transformations to build a large clarity unsigned integer.
- The smart contract will then apply a modulo operation on that large number to limit possible results according to the set difficulty.
For step one, I’m leveraging the City Coin VRF contract: STX Transaction - SPSCW…DYQ11.citycoin-vrf-v2. I believe most implementations will take a very similar approach, but since this was already there and the contract was audited, I felt the best path would be to reuse it.
For step two, I grab the number the VRF contract generated as seed and do the following:
(define-private (pick-lottery-numbers (seed uint))
(if (is-eq difficulty u1) (ok (mod seed u10))
(if (is-eq difficulty u2) (ok (mod seed u100))
(if (is-eq difficulty u3) (ok (mod seed u1000))
(if (is-eq difficulty u4) (ok (mod seed u10000))
(if (is-eq difficulty u5) (ok (mod seed u100000))
(if (is-eq difficulty u6) (ok (mod seed u1000000))
(if (is-eq difficulty u7) (ok (mod seed u10000000))
(if (is-eq difficulty u8) (ok (mod seed u100000000))
(if (is-eq difficulty u9) (ok (mod seed u1000000000))
(if (is-eq difficulty u10) (ok (mod seed u10000000000))
err-invalid-difficulty)))))))))))
In my analysis, I collected this function’s output and plotted it to observe the distributions visually. I also did a statistical analysis using the Chi-squared method, comparing the observed results with those of a uniform distribution (null hypothesis), considering the modulo operation would group results. A p-value of less than 0.05 suggests that the data distribution significantly differs from a uniform distribution. A p-value greater than or equal to 0.05 suggests insufficient evidence to conclude that your data significantly differs from a uniform distribution.
Difficulty 1
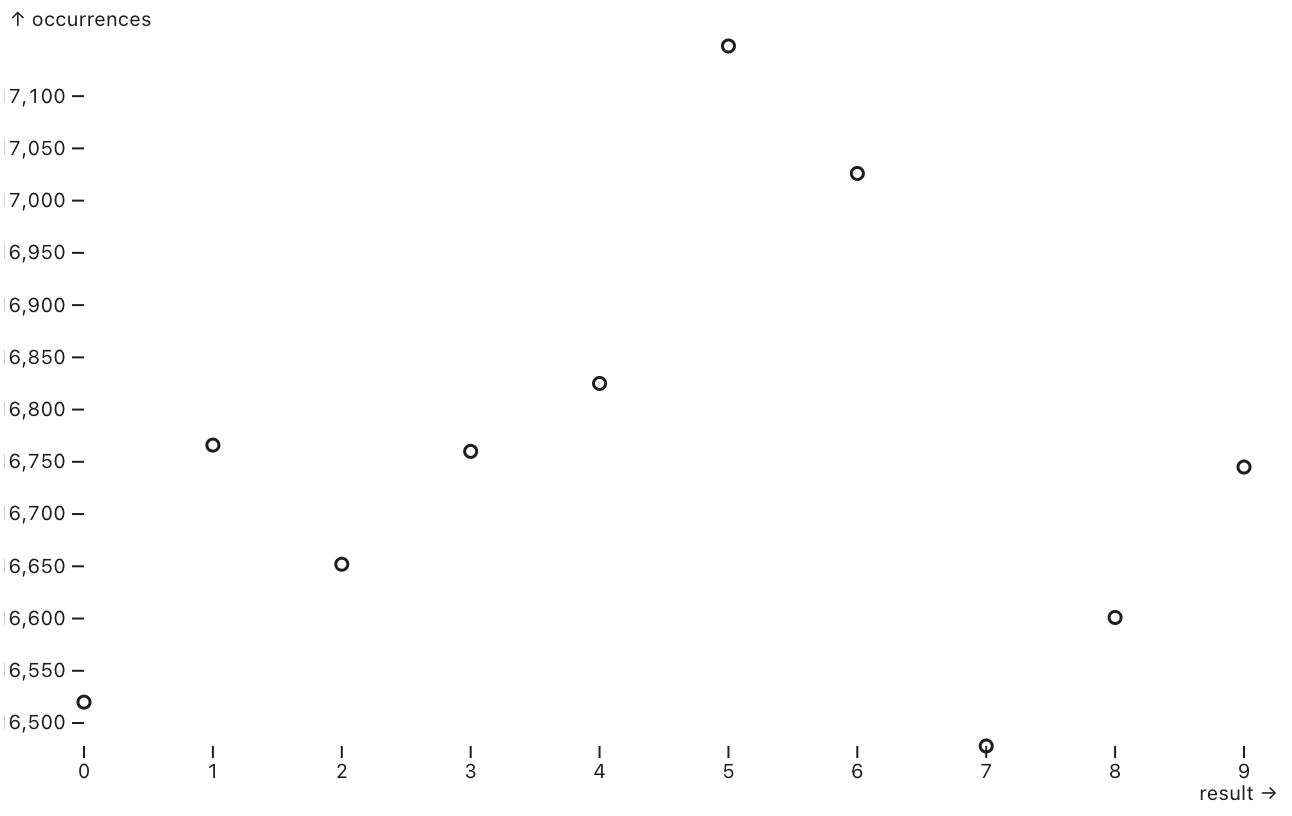
P-value: 0.004575483833877736
Difficulty 2
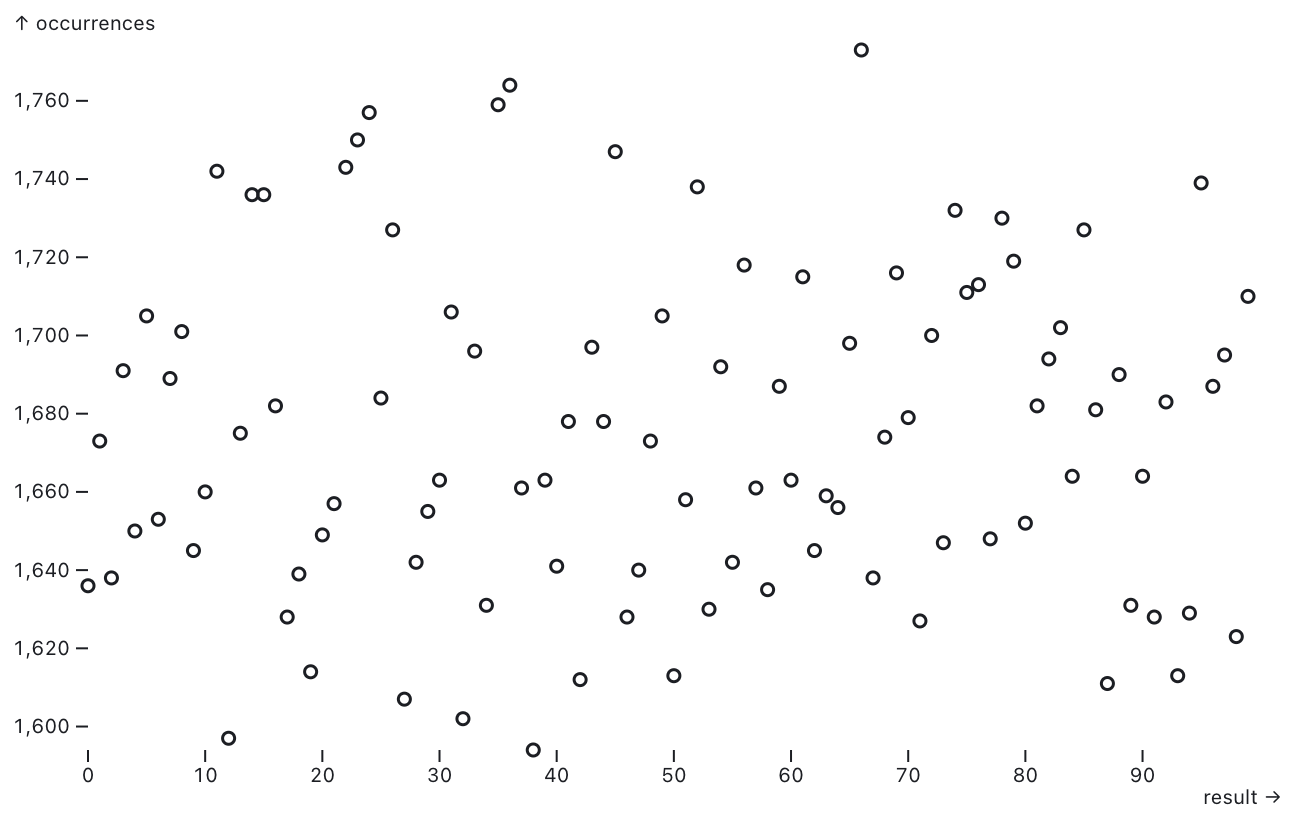
P-value: 0.263850889504435
Difficulty 3
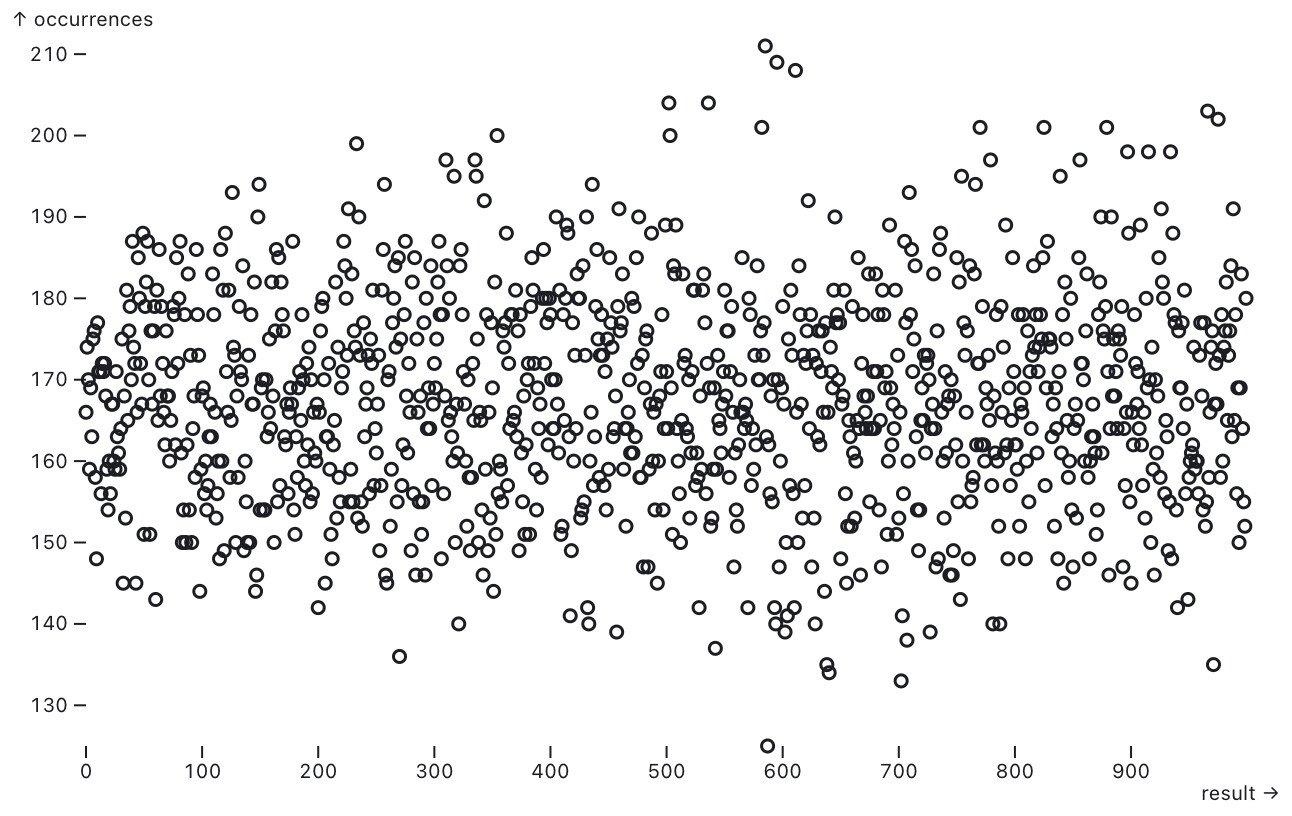
P-value: 0.37192589368491225
Difficulty 4
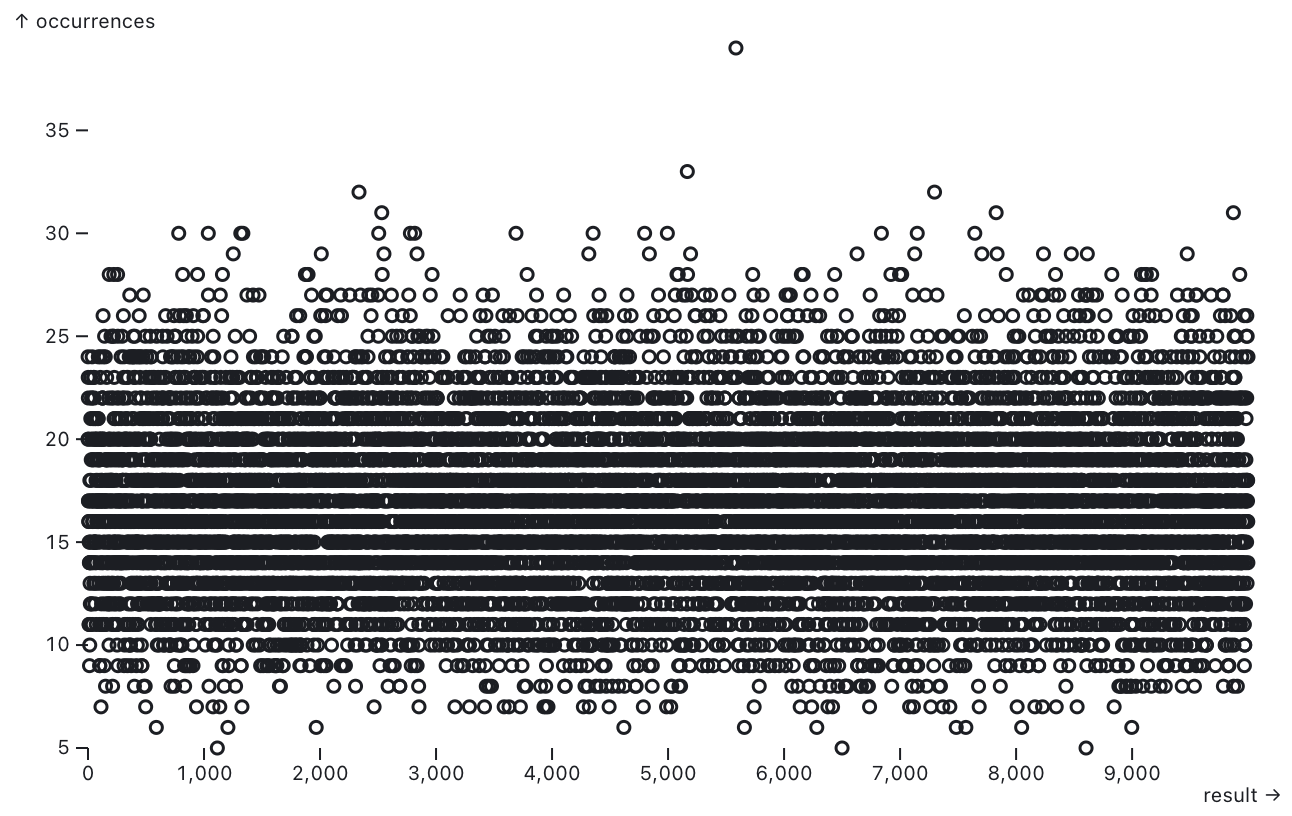
P-value: 0.3905126463210302
For difficulty 5, the uniformity of the results has changed significantly, probably because the sample size has become too small to test (?).
Difficulty 5
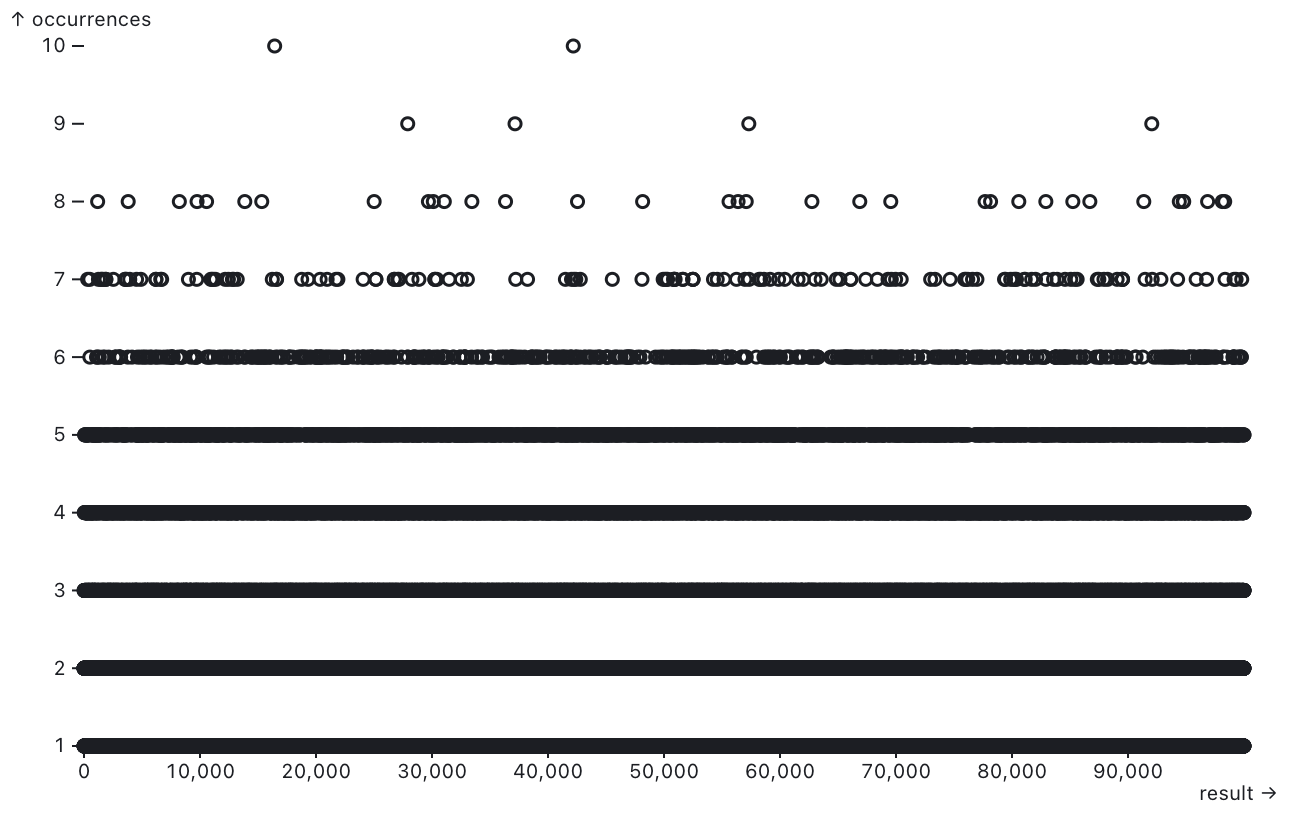
P-value: 1
You can have a look at the data and how every calculation was made here: An analysis of the randomness of the drawing mechanism behind the Felix Lottery Smart Contract / vini.btc | Observable
You can also play with the data. This is how I collected the data: felix-contract/scripts/rnd-analysis.js at main · vini-btc/felix-contract · GitHub
My main questions are:
- Is there something wrong conceptually or in implementing the statistical tests?
- Is there something wrong with implementing the random integer generation in the smart contract?
- Would you consider the results enough to claim the drawing mechanism is fair?
- If I want to increase the confidence that my algorithm outputs are close to a uniform distribution, would adding another “source of randomness” to increase entropy make sense? I was thinking of adding the result from the rnd integer generated by the City Coin contract to something like the block timestamp or the Bitcoin block hash. Still, those probably open the possibility of miners colluding to get a specific result.
In general, any insights or feedback are very welcome!