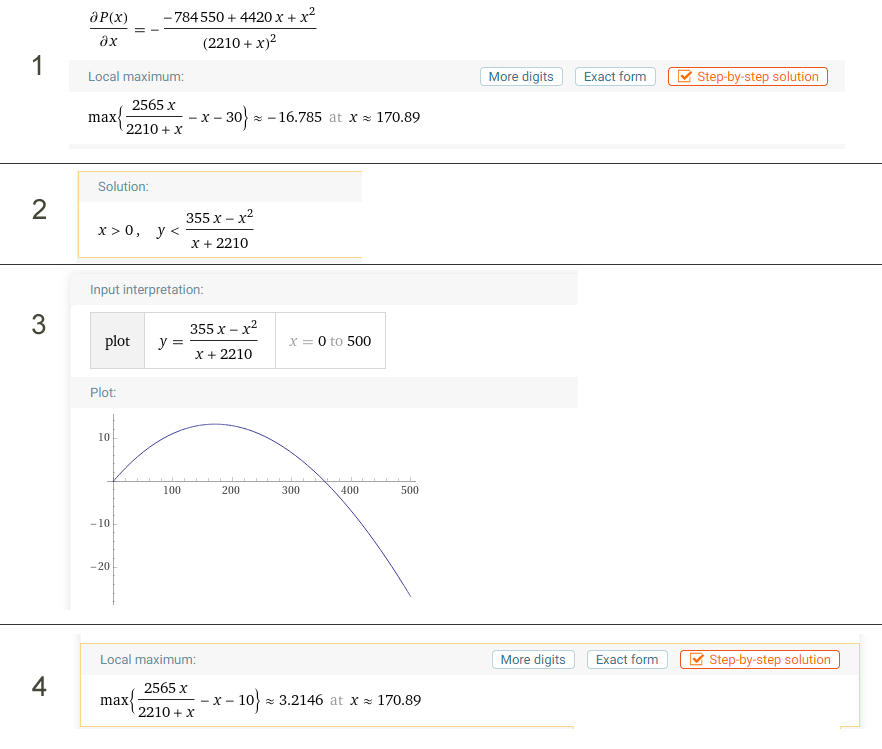
The first reward cycle for earning Bitcoin from consensus is currently on-going on the Stacks blockchain. A reward cycle is 2000 blocks or roughly 2 weeks. The next reward cycle is expected to start in approx 450 Bitcoin blocks. Hiro team is doing an analysis of the first reward cycle using publicly available Stacks blockchain data and we’ll share that here when it’s complete. I wanted to discuss a few quick points:
-
So far 26.93 BTC (~$1.2M USD) has been spent by miners for this cycle. Total reward slots per cycle are 4000, meaning 2 Bitcoin addresses per block are randomly chosen for the rewards based on the stackers who are participating in consensus.
-
Approx 110M STX participated in this cycle taking 44% of the 4000 reward slots, where as 56% of the slots were unoccupied and the corresponding BTC rewards for those slots were burned. Due to certain potential miner incentive corner cases, the minimum level of stacking participation is 25% of the liquid supply and if less than 25% of the supply participates (as we’re currently seeing in the first cycle) then the unoccupied reward slots go to a burn address. If more than 25% of the supply participates in future cycles then we will not see any burn.
-
Given that less than 25% supply was participating and 56% of the reward slots were going to a burn address, stackers noticed more payouts coming to them in the early part of the cycle. This is because all burn slots occur towards the end of the cycle. In other words, only the first 44% slots had rewards going to stackers and the remaining 56% slots towards the end were all burns. If more than 25% of the liquid supply participates then reward addresses for the stackers will be randomly distributed through out the cycle (vs front-loaded at the start of the cycle).
It’s early days of this brand new consensus mechanism (we’re literally in the first reward cycle!) but I’m excited to see the protocol work as intended out in the wild. There is a forum post that summarizes some learnings from Stacking so far. You should check it out and leave any feedback. A reminder that my company, Hiro PBC, does not control the Stacks blockchain and any potential improvements need to go through the SIP process and accepted by independent miners (Hiro is not involved with the SIP committee and is not a miner on the network). Thanks and happy stacking to those who are participating!